生き活き数学教室 解答解説一覧
仙台のコミュニティFM「ラジオ3」にて、毎月第1・3月曜日放送中の「生き活き数学教室」。毎回コーナーの終わりに出す宿題の解説を紹介!
【聞き方】
仙台在住の方:FM76.1Hzにて視聴可能
その他:ListenRadio(リスラジ)より、ネット視聴が可能!
コチラにアクセスして、全国のラジオ局 > 東北 > RADIO3を選択!
  |
第8回:鉛筆と消しゴムの値段 第8回は計算問題!うっかりと引っかからないように注意ですよ! 問題はこちら! 「鉛筆と消しゴムは合わせて150円で、消しゴムは鉛筆より100円高い。鉛筆はいくら?」 50円と即答したそこのあなた!もう一度ゆっくり考えてみましょう! 今回は、中学数学の初歩、「方程式」を使ってみましょう! まずは、求める鉛筆の値段をx円とします。 そうすると、消しゴムの値段もxを使って表すことが出来ますね。 鉛筆より100円高いので、 x+100円になります。 ここまで出来たらあとは計算! 言葉をそのまま式にしましょう。 鉛筆と消しゴムは合わせて150円ですから、 x+(x+100)=150 となります。 これを計算すると、 2x+100=150 2x=150-100 2x=50 x=25 したがって、鉛筆の値段は25円と求めることが出来ました! 久しぶりにがっつり計算した方も多いでしょうか? 方程式は数学の基礎! 覚えておきましょう! では、次回の解説をお楽しみに! (解説者:菅原一真) |
 |
第7回:命題と対偶 第7回の問題は、命題に関する問題! 「『カラスは黒い』はカラスを見ずに証明できる?」 一体何を言ってるんだ!? と感じる人も多いでしょう。 これはいわゆる、「数学的屁理屈」です!(笑) この問題を解くには、高校数学で習う「命題」に関する知識が必要です。 「命題」とは、「これはこうだ」という定義や事柄を指します。 これはなんでも構いません。 「1+1=2」も、「車は走る」も、すべて命題と言えます。 そして、命題には「裏・逆・対偶」が存在します。 「裏」は、全体を否定したものです。 例えば、「車は走る」の裏は、「車でないなら走らない」になります。 「逆」は、前後を逆にしたものです。 例えば、「車は走る」の逆は、「走るなら車」となります。 そして「対偶」は、「裏」の「逆」です。 「車は走る」の対偶は、「走らないならば車ではない」になります。 命題には、「真偽」があり、それを考えます。 「真」とは、その命題は「正しい」ということです。 「偽」とは、その命題は「間違っている」ということです。 例えば、「トンボは昆虫」という命題を考えた時、 確かに「トンボ=昆虫」ですから、この命題は「真」であると言えます。 今度は「ライオンは草食」という命題を考えます。 しかし、「ライオンは肉食」ですから、この命題は「偽」であると言えます。 このとき、「ライオンは肉食」の部分を「反例」と呼びます。 命題が偽のときは、必ず「反例」を挙げなければなりません。 先に話した、「逆・裏・対偶」にも、それぞれ真偽があり、それを考えていくのですが、 この時、「命題とその対偶は、真偽が一致する」という性質があります。 先程の「トンボは昆虫」を考えてみると、 対偶は「昆虫でないならばトンボではない」になります。 この真偽は、「昆虫でない以上トンボである可能性は無い」ことから、 「真」ですよね? この、「命題」「対偶」「真偽の一致」を使うと、 「カラスは黒い」の証明をすることが出来ます。 まずは対偶を取ります。 「カラスは黒い」の対偶は「黒くないならばカラスではない」です。 この世の黒くないもの、つまり、「黒以外の色のものにはカラスは含まれない」ということですね。 確かに、黒くないカラスなんていませんから、反例を挙げることは出来ません。 つまり、「黒くないならばカラスではない」の命題は真と言えます。 そして、「命題とその対偶は真偽が一致する」ことから、元の命題も真。 よって、「カラスは黒い」となるわけです。 どうでしょうか? なんとなく分かったような分からないような・・・ 議論でねじ伏せられているような…(笑) 「数学的屁理屈」と言ったことを感じていただけましたでしょうか。 「カラスは黒い」以外にも、色々なことに使える考え方ですので、 言葉遊びのように試していただければと思います。 では、次回の解説をお楽しみに! (解説者:菅原一真) |
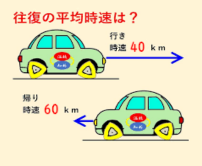 |
第6回:平均速度 第6回の問題は、平均速度に関する問題! 「A地点とB地点を自動車で往復します。行きは時速40km、帰りは時速60kmでした。往復の平均の速さは?」 「簡単じゃん!答えは50kmだ!」 と思ったそこのあなた! 残念ながら間違いですよ! まずは速さについておさらいです。 小学校のときに、速さの求め方を習ったと思います。思い出しましたか? 「み・は・じ」と教わった方も多いのではないでしょうか。 速さを求めるには、「距離」と「時間」が必要です。 速さ=距離÷時間 ですよ!思い出しましたか? ここで問題を見てみると、距離も時間も書いてありませんね。。。 では仮に距離を設定してみましょう。 A地点とB地点の間の距離を120kmとします。 このとき、行きと帰りそれぞれにかかった時間を考えてみましょう。 まずは行きですが、 120kmの距離を時速40kmで走っていますね。 このときかかった時間は、 120÷40=3 ということで、3時間になります。 同じように帰りも考えてみると、 120÷60=2 ということで、2時間になりました。 ここまで来れば平均の速さはもうすぐですよ! 「平均の速さ」は、 「移動した距離」を「移動にかかった時間」で割ることで導き出せます。 今回は、往復で240kmの距離を5時間かけて移動したことになりますから、 240÷5=48 ということで、平均の速さは、 「時速48km」 と導くことが出来ました。 いかがでしたか? 今回はA地点とB地点の間の距離を120kmとしましたが、どんな数字を当てはめても48kmを求めることが出来ます! 気になる方は、距離を「x」などの文字で置いてみて、同じように計算してみてくださいね! では、次回の解説をお楽しみに! (解説者:菅原一真) |
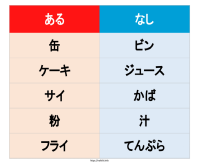 |
第5回:あるなしクイズ 第5回の問題は、あるなしクイズでした! あるに共通するものが何なのか、 なしとの違いは何なのか、 皆さんは気づくことが出来ましたか? 今回の解説では、因数分解に結びつけて考えていきましょう! あるなしクイズの解き方は、共通点を見つけるところから始めます。 「ある」に共通するもの 「なし」に共通するもの 「ある」と「なし」の対比で共通するもの などなど。。。 色々な視点から考えていきます。 まず、「ある」「なし」それぞれ、縦に見たときに共通するものがありそうかというと、 ジャンルも物もバラバラで、見つかりそうにありませんね。 では、横に見て比べてみましょう。 ジャンルは同じで、別のものが書いてあることに気づきましたか? ただ、それでも共通点と言えるほどのものはありませんね。。。 なかなか難しい。 ではここで視点を変えて、「文字」に注目してみましょう。 ある文字が共通して入っていたり、ある言葉が共通して入っていたり。 あるいは、ある文字や言葉をくっつけると違う言葉になったり。 言葉遊びみたいな感覚で考えてみます。 では、ここから因数分解っぽく考えてみましょう。 「X」という文字や言葉をつけたときに別な言葉に変わるかどうか見ていきます。 すると、表はこのようになりますね。 「ある」は、Xをつけても意味が通るはずですから、こちらから考えていきましょう。 缶+X ケーキ+X サイ+X 粉+X フライ+X ここからはひらめき力! Xに入る言葉が「パン」であることに気がつけば、ゲームクリアです! 試しに、「なし」に「パン」をつけてみてください。 意味が通る言葉にはならないのが分かりましたか? 因数分解とは、 ax+bx+cx+dx+ex=x(a+b+c+d+e) とする数学の考え方です。 今回の問題では、 乾パン+パンケーキ+サイパン+パン粉+フライパン=パン(缶+ケーキ+サイ+粉+フライ) と考えられます。 このあたりが「あれ?」という方は、中学数学を勉強し直す必要があるかも・・・? ということで、今回の答えは「パンがつく」でした! この機会に、ぜひ因数分解を思い出して、色々な考え方に応用してみてください! では、次回の解説をお楽しみに! (解説者:菅原一真) |
 |
第4回:紙を何回折れば月まで行ける? 第4回の問題は、紙を何回折れば月まで行ける?という問題でした! なんだか途方も無い話に聞こえますね。。。 実際、月と地球の間の距離は約38万kmあるようです。 計算して考えていきましょう! 前提として、紙の厚さは0.1mmとしておきます。 まずは、1回折るごとにどれくらいの厚さになるか計算してみましょう。 これは簡単ですね。 1回折れば2枚重なるのと同じ状態ですから、 0.1×2=0.2 で、0.2mmになります。 さらにもう一回折ってみましょう。 今度は0.2mmを2枚重ねるのと同じ状態ですから、 0.2×2=0.4 で、0.4mmになります。 ここで、数字ではなく計算方法に注目してみます。 0.1に対しての掛け算として考えてみると、 1回折ったときは、0.1に2を1回かけ、 2回折ったときは、0.1に2を2回かけていることが分かります。 折る度に2倍、さらに2倍となっているわけですね。 数学では、これを2のべき乗、指数関数と言います。 べき乗、指数関数がどれほどすごいのか、実際に計算してみましょう。 5回ほど折ったとすると、2を5回かけることになるので、 0.1×2^5=0.1×32=3.2 なんと、元の32倍になりました! では、更に5回折ってみるとどうでしょうか。 計算は 0.1×2^10=0.1×1024=102.4 ですから、なんと1024倍です! たった5回で30倍以上、、、 10回だと1000倍を超えてしまうのです。 掛け算とは恐ろしいですね。。。(苦笑) べき乗の凄さ、恐ろしさがわかったところで、本題に戻りましょう。 月に達するまでの回数は一体どれくらいになるのでしょうか。 月までは38万kmでした。 これに近づけるためには、やっぱりたくさん折らないといけない気がしますが、 10回で1024倍ですから、 さらに10回折ればさらに1024倍、更に折れば、、、 と続いていきます。 途方もない数ですね。。。汗 実際に計算してみましょう。 20回折ると、 0.1×2^20=104857.6(10万4857.6)=10.48576m 30回では、 0.1×2^30=107374182.4(1億737万4182.4)=107.3741824km 40回では、 0.1×2^40=109951162777.6(1099億5116万2777.6)=10万9951.1627776km 40回で、約10万kmの厚さまでたどり着くことが出来ました。 ここから更に2回ほど折れば、約40万kmとなり、月までの距離を超えることが出来ます。 ということで、答えは、 「42回」 でした! 掛け算、べき乗、指数関数の凄さ、恐ろしさが分かる問題でしたね(笑) では、次回の解説をお楽しみに! (解説者:菅原一真) |
 |
第3回:40人クラスの中に同じ誕生日の人がいる確率は? 第3回の問題は、40人クラスの中に同じ誕生日の人がいる確率は?という問題でした! ぱっと見は、「え?そんなのほとんどありえなくない?」と思うような問題ですが、 実際に数学的に考え、計算していくと、なんと8割以上の確率で同じ誕生日の人がいるという結果になります! 実際の計算とともに考えていきましょう! まず、この問題では、日本語の意味を改めてじっくり考える必要があります。 40人クラスの中に「同じ誕生日の人がいる」のと、 40人クラスの中に「自分と同じ誕生日の人がいる」のでは、 全然違う意味になるのは分かりますか? 前者は、40人の内の誰かと誰かが同じ誕生日であればいいことになりますが、 後者は、自分と自分以外の39人の内の誰かが同じ誕生日である必要があります。 では先に、後者の「自分と同じ誕生日の人がいる」確率から考えてみましょう。 うるう年のことは例外として、一旦置いておきます。 誕生日は1年の内のどこか1日です。自分の誕生日を、「◯月×日」としておきます。みなさんはここに自分の誕生日を当てはめてくださいね。 ここから、自分以外の39人の誕生日が自分と同じ誕生日である確率を考えていきますが、このままだと数学的に数字で表しにくいので、逆のことを考えます。 確率は、起きる現象それぞれの確率をすべて足すと必ず100%になる性質があります。 単純なくじ引きで考えてみるとわかりやすいですね。 5本の内1本が当たりのくじを1回引くとき、あたりを引く確率は20%で、ハズレを引く確率は80%ですよね。 同じように、誕生日についても考えてみましょう。 「自分以外の39人の内の誰かが自分と同じ誕生日」の逆は、 「自分以外の39人全員が自分と違う誕生日」です。 自分と同じ誕生日である確率は、365日の内の1日ですから、1/365になります。 ということは、自分と異なる誕生日である確率は、364/365ですね。 つまり、自分以外の39人全員が自分と違う誕生日である確率は、 (364/365)×(364/365)×(364/365)×・・・ を、39回繰り返せばOKです。 実際に計算してみると、約90%になります。 ということは、「自分と同じ誕生日の人がいる確率」は、90%の逆である、10%ということになります。 この数字だと、なんだか実際の経験や体感に近い感じがしますよね。 では今度は、「同じ誕生日の人がいる」確率を考えてみましょう。 先程と同様、逆のことを考えてみます。 「同じ誕生日の人がいる」の逆は、 「全員が異なる誕生日」です。 40人を一度に考えるのは大変なので、1人づつ考えていきましょう。 1人目はまだ比べる対象が居ないので、一旦そのまま。 2人目からが計算のスタートです。 2人目は、1人目と異なる誕生日であればいいので、確率は364/365です。 次に3人目。 3人目は1人目、2人目のどちらとも異なる誕生日である必要があるので、確率は363/365です。 したがって、 4人目は362/365 5人目は361/365 ・ ・ ・ という感じで考えていけますね。 これを実際に40人分計算してみると、約11%になります。 ということは、「同じ誕生日の人がいる確率」は、その逆の約89% 8割どころか9割近い確率になるわけです。 さっきとは全然違う結果になりましたね。 びっくりした方も多いのではないでしょうか。 数学のびっくりももちろんですが、言葉の勘違い一つで全然見当違いになってしまう可能性もある日本語の使い方にも気をつけなきゃいけないということも、言えるかもしれませんね。 今回の解説は以上となります。 もし、「まだわからないんだけど。。。」という方は、メールなどで気軽にお問い合わせください。 では、次回の解説でお会いしましょう! (解説者:菅原一真) |
 |
第2回:嘘つきと正直者 第2回の問題は、発言から嘘つきと正直者を見極めて、正直者を当てる問題でした! どんな問題かというと、、、 3人の内一人が正直者で残りの二人はうそつきです。 次の会話から正直者を見つけ出してください。 A「私は正直者です。」 B「Aはうそつきです。私が正直者です。」 C「Bはうそつきです。本当の正直者は私です。」 という、問題です。 それぞれ一言づつしか喋っていませんが、1つずつ考えていくと正直者を導き出すことが出来ます。 論理問題を考えていくポイントは、地道ですがパターンをそれぞれ検証して矛盾が生じないかを考えていくことです。 まず最初に、Aが正直者だった場合を考えてみましょう。 Aは正直者ですから、自分のことを正直者というのは矛盾していませんね。 他の二人はどうでしょうか。 Bは嘘つきですから、Aのことを嘘つきと言い、自分のことを正直者だと言います。 これも矛盾は生じていません。 ではCはどうでしょうか。 Cは嘘つきですから本当のことは言いません。 しかし、「Bは嘘つきである」と、本当のことを言ってしまっていますね。 Cが嘘つきなら、Bのことを正直者だと言わなければ矛盾が起きてしまいます。 矛盾が生じたということは、最初に考えていた「Aが正直者」のパターンではないということになります。 では次に、Bが正直者だった場合を考えてみましょう。 Aは嘘つきですから、自分のことを正直者だと言います。 これに矛盾はありません。 次にBは正直者ですから、Aは嘘つき、自分は正直者だと言います。 これにも矛盾はありません。 Cはどうでしょうか。 Cは嘘つきですから、Bは嘘つき、自分が正直者だと言います。 これも矛盾していませんね。 つまり、論理的に噛み合ったということは、「Bが正直者」という最初に考えたことが正しいことになります。 答えは出ましたが、Cが正直者だった場合も考えてみましょう。 AとBは嘘つきですが、Bの発言がAが正直者だった場合のCと同じパターンになっています。 Bが「Aは嘘つき」と本当のことを言ってしまっていますね。 よって、「Cが正直者」のパターンも間違いということになります。 簡単ですが、解説は以上となります。 もし、「まだわからないんだけど。。。」という方は、メールなどで気軽にお問い合わせください。 では、次回の解説でお会いしましょう! (解説者:菅原一真) |
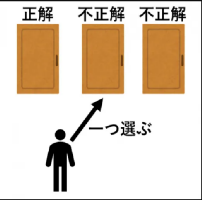 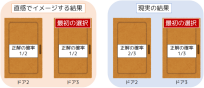 |
第1回:モンティ・ホール問題 第1回の問題は、モンティホール問題。数学界でも物議を醸しがち?な問題でした。 どんな問題かというと、、、 3つの扉があり、1つは当たり、2つははずれとなっています。あなたは、まず3つのうち1つの扉を選びます。 すると、選ばれなかった2つの扉のうち、はずれを1つ取り除かれます。 ここであなたは、扉を選びなおすことができますが、より当たりを選ぶ確率を上げるためには、扉を選びなおすべきでしょうか?それともそのままにしておくべきでしょうか? という、問題です。 一見すると結局1/2なんだから、どっちでも変わらないんじゃ?と感じる人も少なくないと思います。 しかし、大きな違いがあるんですよ! では、段階を追って確率を考えてみましょう。 まず最初に、3つの扉から1つを選ぶ瞬間では、当たりを引く確率は1/3ですね。 このとき、選ばなかった2つのどちらかに当たりがある確率はどれくらいでしょうか? はい、2/3ですよね。 ここが重要ポイントです。 これを踏まえて次に行ってみましょう。 そして、選ばれなかった2つのうち、はずれの扉が1つ外されます。 これで扉は2つになりました。 この時の当たりの確率を考えてみましょう。 あなたが最初に選んだ扉は、特に変わっていませんから、1/3のままです。 では、残った扉はどうでしょうか? 実は、残った扉のあたりの確率は2/3なんです。 最初の時点で、選ばれなかった2つの扉どちらかに当たりがある確率は2/3でした。 はずれの扉が1つ外されたとき、この「2/3」の確率の説明は、 「選ばれなかった2つの扉」から「選ばれなかった1つの扉」に変わります。 そうして、この最終的な2択は、純粋な1/2ではなく、「1/3の扉」と「2/3の扉」になるわけです。 簡単ですが、解説は以上となります。 もし、「まだわからないんだけど。。。」という方は、メールなどで気軽にお問い合わせください。 では、次回の解説でお会いしましょう! (解説者:菅原一真) |
現在も受検者募集中!君も合格して名前を連ねよう!
